ubersite.blogg.se

1. #Binary sequences which are eventually zero full#
2. #Binary sequences which are eventually zero code#
3. #Binary sequences which are eventually zero series#

Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: "provided those objects be capable of a twofold difference only as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature". In 1605 Francis Bacon discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text. The ordering is also the lexicographical order on sextuples of elements chosen from a two-element set. In the 11th century, scholar and philosopher Shao Yong developed a method for arranging the hexagrams which corresponds, albeit unintentionally, to the sequence 0 to 63, as represented in binary, with yin as 0, yang as 1 and the least significant bit on top. The residents of the island of Mangareva in French Polynesia were using a hybrid binary- decimal system before 1450. The Indian scholar Pingala (around 5th–2nd centuries BC) developed a binary system for describing prosody in his Chandashutram. Slit drums with binary tones are used to encode messages across Africa and Asia. The binary system of the I Ching, a text for divination, is based on the duality of yin and yang. The aforementioned I Ching that Leibniz encountered dates from the 9th century BC in China. īinary systems predating Leibniz also existed in the ancient world. During this time period, Leibniz had not yet found a use for this system.

He created a system consisting of rows of zeros and ones.

#Binary sequences which are eventually zero series#

The book had confirmed his theory that life could be simplified or reduced down to a series of straightforward propositions. After his ideas were ignored, he came across a classic Chinese text called I Ching or ‘Book of Changes’, which used 64 hexagrams of six-bit visual binary code. Leibniz was trying to find a system that converts logic verbal statements into a pure mathematical one. He believed that binary numbers were symbolic of the Christian idea of creatio ex nihilo or creation out of nothing. īinary numerals were central to Leibniz's theology. Leibniz saw the hexagrams as an affirmation of the universality of his own religious belief. Leibniz encountered the I Ching through French Jesuit Joachim Bouvet and noted with fascination how its hexagrams correspond to the binary numbers from 0 to 111111, and concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical visual binary mathematics he admired. Leibniz's system uses 0 and 1, like the modern binary numeral system.

#Binary sequences which are eventually zero full#

The full title is translated into English as the "Explanation of the binary arithmetic", which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi. The modern binary number system, the basis for binary code, was invented by Gottfried Leibniz in 1689 and appears in his article Explication de l'Arithmétique Binaire. For example, the lower case a, if represented by the bit string 01100001 (as it is in the standard ASCII code), can also be represented as the decimal number "97".

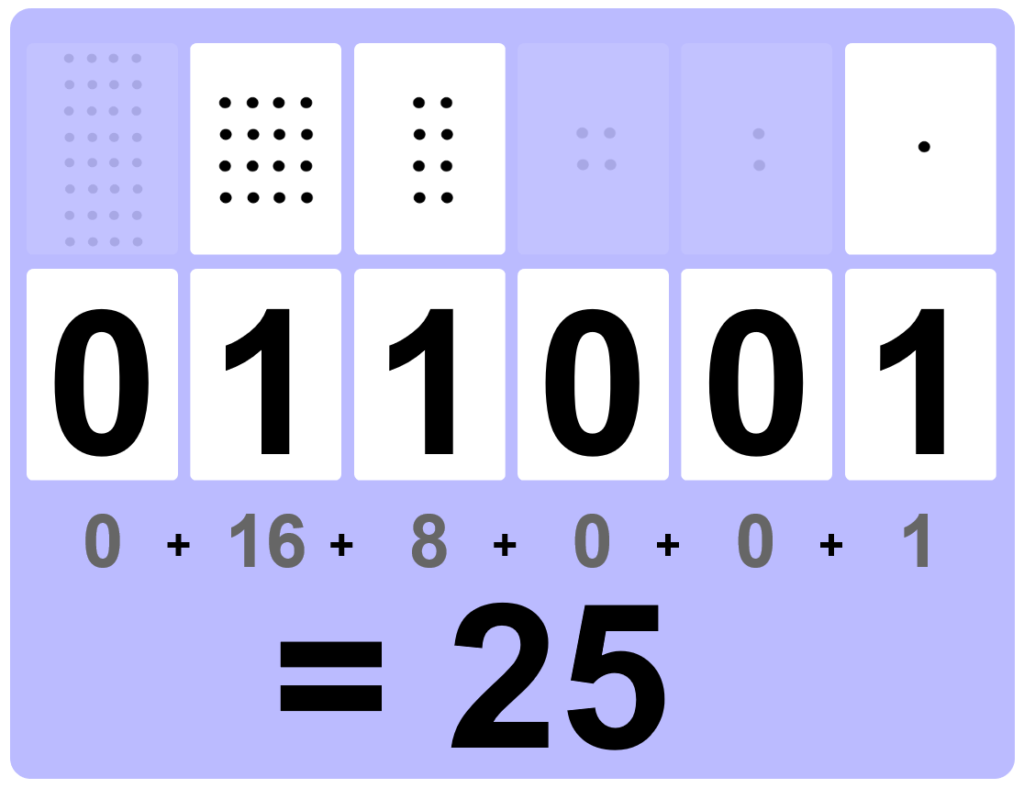
There are many character sets and many character encodings for them.Ī bit string, interpreted as a binary number, can be translated into a decimal number.

#Binary sequences which are eventually zero code#

In a fixed-width binary code, each letter, digit, or other character is represented by a bit string of the same length that bit string, interpreted as a binary number, is usually displayed in code tables in octal, decimal or hexadecimal notation. Those methods may use fixed-width or variable-width strings. In computing and telecommunications, binary codes are used for various methods of encoding data, such as character strings, into bit strings. For example, a binary string of eight bits (which is also called a byte) can represent any of 256 possible values and can, therefore, represent a wide variety of different items. The binary code assigns a pattern of binary digits, also known as bits, to each character, instruction, etc. The two-symbol system used is often "0" and "1" from the binary number system. The word 'Wikipedia' represented in ASCII binary code, made up of 9 bytes (72 bits).Ī binary code represents text, computer processor instructions, or any other data using a two-symbol system.